
Visitors enter the virtual gallery through what appears to be a wormhole before arriving in a room where every wall is covered by psychedelic works of art—whorls of pink, yellow, and green in shapes like coiled springs, some of which vibrate and move when viewed from the right angle.
The art is both real and not real—a digital representation of an abstract concept—minted on the blockchain and hosted in an online, video-game-like platform by Robert Ghrist, the Andrea Mitchell University Professor of Mathematics and Electrical & Systems Engineering.
With appointments in both the School of Arts & Sciences and the School of Engineering and Applied Science, Ghrist’s penchant for combining seemingly disparate domains and interests extends to every part of his work.
According to Vidit Nanda, a professor of mathematics at Oxford and one of Ghrist’s many former postdoctoral fellows, Ghrist has “the soul of an artist trapped in the body of a scientist.” An aficionado of William Blake, Ghrist is equally at home discussing Dante, open-world video games, and the Hopf fibration, the abstract shape depicted in his virtual gallery.
Nanda says Ghrist’s distinctive combination of aesthetic flair—including his preference for wearing suits, even in sweltering Philadelphia summers—and mathematical rigor makes him a singular figure in the world of applied mathematics. “Every paper, every talk slide, every calculus video carries his unique signature, and you can immediately recognize his work,” says Nanda. “It’s like encountering a Van Gogh painting or a Bach fugue—you immediately know who made it.”

An unlikely mathematician
Growing up in suburban Ohio, Ghrist never pictured himself becoming a mathematician—the field felt impenetrable. “I was bored in school, trying to read math books that were way too advanced and just not getting it,” Ghrist recalls. “It wasn’t until I went to university that the world just opened up for me.”
He might have remained an engineer, if not for a particularly inspiring calculus professor at the University of Toledo. “He was your canonical weird mathematician,” says Ghrist. “But I just fell in love with the subject.”
Hardly anyone in Ghrist’s family had attended college, so pursuing a doctorate didn’t occur to him at first. “It just wasn’t the kind of thing someone like me would do.”
From equations to accolades
Today, Ghrist has received some of the most prestigious accolades in mathematics and science. Named a Presidential Early Career Scholar by President George W. Bush and one of the 50 most innovative researchers in the world by Scientific American, Ghrist has also been recognized by the Mathematical Association of America for the unusual clarity of his writing, with the Chauvenet Prize. He has authored dozens of papers and more than a half dozen books and has been awarded millions of dollars in grants to study applied mathematics in contexts as varied as networks and the analysis of public opinion.
Ghrist has been equally celebrated for his impact in the classroom. An inaugural faculty co-director of Penn First Plus, which supports first-generation students, Ghrist has received both the Lindback Award—Penn’s highest honor for teaching—and the S. Reid Warren Jr. Award, Penn Engineering’s highest teaching honor.
“Rob has an extraordinary gift for making the abstract not just accessible, but exhilarating,” says Tony Pantev, a professor and chair of the Department of Mathematics. “He shows students—especially those who may not have seen themselves as mathematicians—that mathematics is not a closed door, but an open world full of beauty, creativity, and possibility.”






1/6
PIK Professor in the School of Arts & Sciences and School of Engineering and Applied Science Rob Ghrist is known not only for his mathematical, engineering, and teaching prowess, but also for his striking digital illustrations. This graphic by Ghrist depicts the Lorenz attractor, a simple mathematical model whose butterfly‑shaped loops illustrate the “butterfly effect,” where tiny changes in starting conditions lead to vastly different outcomes.Previous SlideNext Slide
The shape of data
Shortly after beginning his tenure at Penn in 2008, Ghrist’s name became synonymous with the burgeoning field of topological data analysis, a mathematical subfield where number crunching and abstract shapes converge.
Ghrist’s pioneering work broke new ground in both abstract math theory and everyday problem-solving. He created mathematical tools that work for different types of data, making his methods versatile across different fields. Some data resembles smooth, flowing landscapes, continuous data, while other data looks more like distinct building blocks with clear edges, discrete data.
“The area of mathematics that I work in is so visually grounded that in order to really understand something, I often need to draw a picture of it and get it just right,” explains Ghrist.
Imagine a Venn diagram: One circle is topology—studying spatial properties unchanged by stretching or bending—and the other is data analysis—hunting patterns in numbers. At their intersection, Ghrist and his colleagues forge tools that address both pure‑math questions and real‑world problems.
Topology focuses on qualitative features—connections, holes, and twists—rather than lengths or angles. Consider a square, a circle, or a dodecahedron: What matters are the number of holes, how regions connect, and how boundaries arrange.
This approach revolutionized problem-solving, famously illustrated by mathematician Leonhard Euler’s solution to the Seven Bridges of Königsberg problem, wherein citizens tried crossing each of the town’s seven bridges exactly once. Euler recognized that distances were irrelevant—only connections mattered.
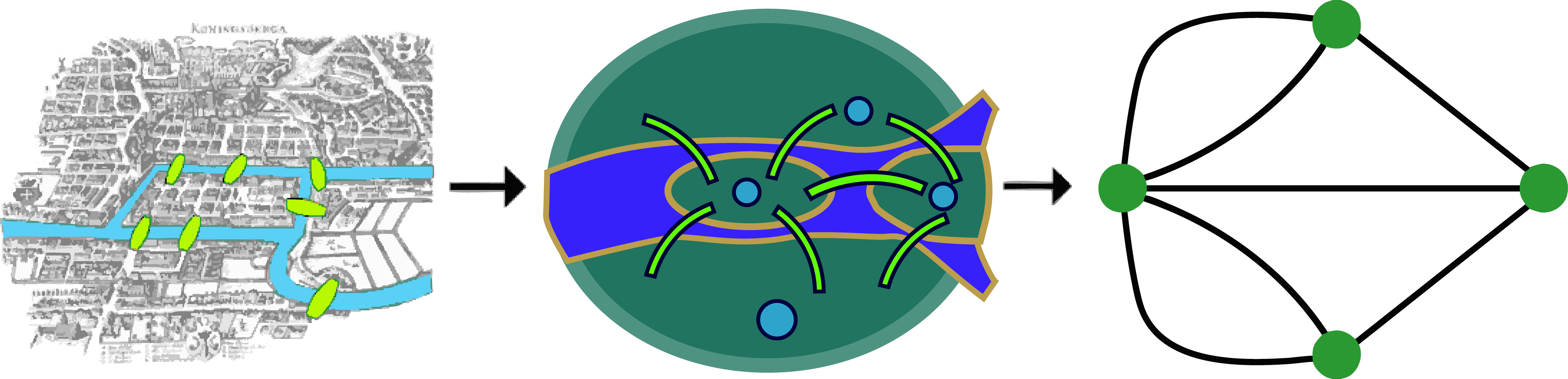
By representing landmasses as nodes and bridges as edges, Euler proved that the task was impossible because it lacked the necessary condition of having exactly zero or two nodes with odd connections.
Ghrist applies a similar school of thought to data analysis. “You have a bunch of data points in a point cloud,” he says, “and it has some sort of shape. If you can look at it, if you could see it, if you can grab it with your hands and rotate it around like you would do on a computer screen, then you can see what the shape is.”
But real-world data rarely presents itself so neatly. “If that data is very high-dimensional, or if it’s really noisy and you’re not sure what the coordinates of these points are—or if there aren’t coordinates—how do you get at the shape?” Ghrist asks. “Topological data analysis aims to get at a notion of shape that is independent of how you can represent or express the points visually.”
Applying these tools in a paper published in 2019, Ghrist and his collaborators tackled one of the most challenging problems in topological data analysis: comparison across datasets. Ghrist explains the approach, “If I’ve got a data set and I find a hole in it, maybe I find a couple of holes, and then I run the experiment again and I get a new data set and I find some holes in that—how can I compare them and see if I find the same holes or are they different?”

This approach represents a significant evolution in mathematical thinking. Where traditional calculus was developed to solve physics-based problems in two and three dimensions—designing efficient airplane wings or launching satellites—Ghrist notes, “We’ve solved all those problems. Today’s problems are data. Genetics. Huge multidimensional environmental models. AI and neural networks with billions of parameters.”
The triple-integral shaman
As a teacher, Ghrist is no less inventive. The same creativity and zeal that he brings to research follow him to the classroom. Whether producing hand-drawn animations or redesigning the entire Penn calculus sequence, Ghrist constantly looks for ways to engage students. “His lectures held us spellbound three days a week,” recalls Nanda, the Oxford professor. “He was always hinting about the deeper topics to come, like some Triple Integral Shaman.”
Despite his renown as a mathematician, Ghrist is equally committed to teaching undergraduates, graduate students, and postdoctoral fellows. “He puts a lot of effort into making sure that every incoming student has a chance to succeed at Penn,” says Iris Yoon, assistant professor of mathematics at Wesleyan University and one of Ghrist’s former graduate students.
Ghrist is also committed to teaching mathematics to students in Penn First Plus who might not have had calculus before college. “He tries to make sure that the undergraduate students entering Penn have a solid understanding of calculus,” says Yoon, “so that they can do well in whatever field they pursue.”
As a research mentor, Ghrist emphasizes originality, urging advisees to eschew “least publishable units”—the smallest, most incremental ideas that journals might accept—in favor of more substantial contributions. “One of the things Rob taught me is not to read the literature too religiously,” says Hans Riess, a research scientist at Georgia Tech. “If you read papers all day, you’ll think the way that everyone’s been thinking.”
Indeed, Ghrist is more than happy to plunge into areas of mathematics with which he is unfamiliar. “Rob is willing to learn alongside his advisees,” notes Darrick Lee, a Chancellor’s Fellow in the School of Mathematics at the University of Edinburgh. “He never says, ‘This is my area of expertise, and I sit within it, and I will invite you inside,’ but rather, ‘Let’s go exploring together and find out new things.’”
The next generation: Ghrist’s mathematical heirs
While Ghrist’s work on comparing topological features across datasets has advanced the field, the many scholars he has mentored see his lasting impact in the new generation of mathematicians applying topological thinking to problems from opinion dynamics to high‑dimensional shape analysis.
Julian Gould’s journey embodies Ghrist’s blend of theory and application. After graduating with a bachelor’s degree in math from Johns Hopkins, Gould detoured into finance as a quantitative analyst at T. Rowe Price. “David Giroux, a really brilliant investor, would come to me and say, ‘I have this feeling about this thing based on these ideas. Math boy, what do the numbers say?’” Gould recalls. “I’d find a way to turn that into an actual quantifiable thing.”
He turned those intuitions into data-driven insight. Today, as a Ph.D. candidate in Ghrist’s lab, he studies cellular sheaves—frameworks for how information flows through networks—to model opinion dynamics. “I work on structures that can be applied to how opinions spread,” he explains, extending Ghrist and former student Jakob Hansen’s foundational work by representing beliefs as probability ranges rather than as fixed-point possibilities—much like how real people hold really complex, uncertain views rather than simple yes-or-no positions.
Ghrist’s support went beyond mathematics. “When I told Rob I wanted to leave academia for industry, he was nothing but supportive,” Gould says. “He showed me doors I wouldn’t have known about.”
Miguel Lopez arrived as a Ph.D. candidate in the height of COVID lockdowns. Drawn by Ghrist’s applied topology, he found community in weekly virtual lab meetings. Lopez works in category theory—a “Rosetta Stone of math” that translates ideas across domains—to reimagine linear programming in new contexts. In collaboration with Ghrist and Gould, they wrote a short paper about bottleneck duality, Lopez says.
“One of the really interesting things about this paper is that we got AI to prove the main result. It failed many times—it would just say false things or hallucinate some property. But with a model update, it did eventually get it right, finding a new approach.”
Shreya Arya, who joined as a postdoctoral researcher last fall, co-taught calculus with Ghrist in her first semester. What struck her most was his willingness to embrace innovation in an area as traditionally rigid as calculus instruction. “When you’ve been doing something for a long time, to the extent it becomes second nature, you can get stuck in your ways. I don’t see that in Rob.”
Having worked with Justin Curry—one of Ghrist’s former doctoral students—during her graduate studies, Arya’s arrival at Penn represents a “mathematical homecoming.”
“I always knew of Rob’s work, and I was always very excited by it. It was really my dream to be here,” Arya says.
Together, the three new lab mates bring fresh perspectives to classic optimization problems. Lopez describes what they work on in category theory as a “mathematical Rosetta Stone-like translator” because it helps connect ideas across different mathematical territories, allowing the team to reimagine traditional techniques and unify concepts.
What bridges their work is the recognition that the most interesting problems live at the intersections, Arya reflects. She says Ghrist has taught his mentees great, new ways to think about mathematics—such as how its applications aren’t isolated in neat compartments and that ideas can flow across boundaries.
Featured People
Associate Dean, Undergrad Education; Andrea Mitchell University Professor, Mathematics & Electrical/Systems
